螺栓连接结构广泛应用于航空航天、铁路运输等大型复杂装备中,其连接结构处于复杂装备内部,工作时无法实时监测性能状态[1-3]。同时设备间存在大量结构跨尺度和非线性问题,导致分析螺栓连接结构动力学响应较为困难,对装备的可靠性、安全性造成了困扰。研究学者将有限元方法(FEA)广泛应用到复杂装备的性能计算、压强表征中可通过有限元软件建立螺栓连接结构接触模型分析其性能,弥补无法直接测量的困难。
装备在存储、运输、使用过程,由于振动、碰撞等因素,导致装备受到切向外力的影响,进而影响装备接触状态。接触状态的变化研究对保障结构安全、预测和评估结构寿命、优化结构设计具有重要意义。局部接触区域和压强过高,可能导致复杂装备发生疲劳、塑性形变,影响整个结构的安全[4]。因此,对切向外载荷作用下的螺栓连接接触状态分析具有重要作用。
研究学者将接触边界分为圆形[5]、椭圆形[6]。无切向外力时,接触边界为圆形。随切向力的作用,接触边界逐步演化为椭圆形。接触压强分布可表征为赫兹压强分布、Fernlund压强分布、线性压强分布等。Li[7,8]利用粗糙表面的赫兹压强分布表征接触表面的压强变化,构建了密度函数,并通过实验验证了方法的正确性。此方法能较好表征接触面压强分布规律,但其未知参数较多,导致计算较为复杂。Wang[6]基于Fernlund压强4次分布函数,研究了随切向力变化的动态压强分布函数,分析了接触状态变化。但计算公式较为复杂,待辨识参数较多。
Zhao[5]假设研究了参数较少的线性压强分布,构建了不考虑接触状态演化的线性压强分布函数。因此,急需建立可准确表征连接界面接触边界、面积的数学函数,表征接触边界变化规律。构建考虑切向载荷影响的动态压强分布函数,将接触状态演化引入到分布函数中。
综上,切向载荷作用下连接界面产生接触边界、压强分布变化,对动力学特性造成一定影响。为简化压强分布函数,提高函数预测的准确性,本文建立了高精度有限元模型,研究了接触边界变化规律,分析结合面的多种压强分布函数。构建了参数较少、表征效果较好的切向力动态变化线性压强分布函数。有助于为螺栓连接的力学行为和接触机理提供理论支撑。
1、简化螺栓和平板建模方法研究
混合载荷耦合作用下,螺栓连接与平板接触面受力情况如图1所示。核级设备具有特殊性、复杂性,其内部存在大量螺栓连接结构。以复杂装备中高强度合金镍钢材料为基础,镍钢平板具有高强度、高硬度、耐腐蚀性的特点,广泛应用于航空发动机等多种重要的复杂装备中。然而,由于填充系数较低,现有普通装备中较少使用此材料,目前领域内对于镍钢材料的研究较少。因此,本文聚焦于复杂装备中镍钢结构,以L形平板为对象,简化了装备的复杂程度,避免其它部件对动力学特性产生影响。选取GB/T5783-2016[9]标准的8.8级M8×36标准外六角螺栓作为研究对象。

1.1螺栓紧固件建模
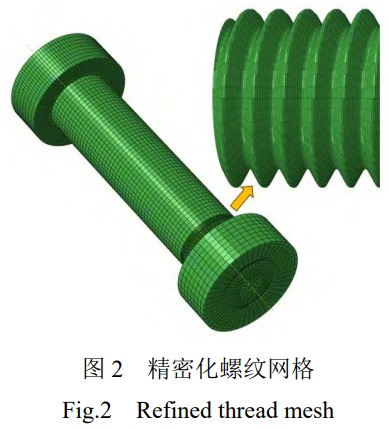
基于Solidworks软件建立带升角螺栓,将螺纹与螺母的相互作用通过ABAQUS软件啮合,可模拟螺栓工作时的受力方向,提高分析的准确性。基于螺栓中性面添加预紧力,可简化计算的复杂程度。螺距P为1mm,螺栓头部内切圆半径为6.5mm,厚度k为5.15mm,对角长度e为14.38mm。为简化螺纹建模复杂程度,提高ABAQUS分析效率和收敛性,采用光滑螺杆替代螺纹并将螺栓头部简化为圆面。网格质量极大影响计算结果,ABAQUS软件可自动划分四面体、六面体网格。螺纹处网格与平面处不同,存在多处的凹凸面。因此,本文采用Hypermesh软件对螺纹处进行手动绘制高精密网格,确保每一处网格呈现均匀六面体形状,如图2所示。精密网格可避免模型不收敛的问题,有效控制计算误差。
1.2等效连接平板建模
为避免转矩对螺栓产生的影响,将平板简化为L形,如图3所示。平板的孔需略大于螺栓直径。因此将平板的螺孔直径调整为9mm,保证平板未受力前,二者不接触。通过ABAQUS自带网格编辑器,调整镍钢平板的网格为四面体网格,对螺栓头部、螺孔接触面进行网格细分,提高计算精度。将材料假定为纯弹性,当外力工作结束后,材料不存在残余形变,可恢复为原状态。设置材料的泊松比为0.291,屈服应力590MPa,弹性模量为205.9GPa,杨氏模量143GPa。

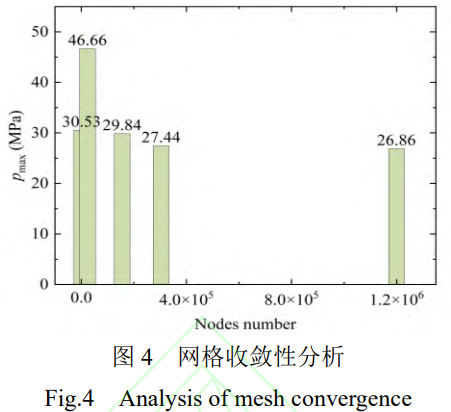
为提高计算的准确性,对模型进行了网格检验,模型节点数量与最大接触压强的关系如图4所示。分别划分了0.5mm、0.8mm、1mm、2mm、5mm单元尺寸的网格。当网格大小为0.5mm-0.8mm时,最大压强趋于稳定在26-27MPa,表明模型网格已趋于稳定,精确度较高。然而0.5mm单元节点数量较0.8mm单元节点数量增加了89万,降低了计算效率。因此采用0.8mm单元尺寸的网格。
1.3有限元载荷、边界条件及分析步设置
ABAQUS软件中施加螺栓预紧载荷的方式有多种:①在螺栓中性面添加固定当前长度的预紧载荷。②基于热膨胀原理采用降温法,通过施加螺栓负温度的形式,使得螺杆收缩产生预紧力。③基于螺纹与螺母的啮合,通过旋转螺母的形式施加预紧。④直接压缩螺杆的长度,使螺杆具有法向的压缩力,即可表征为预紧载荷。上述方法中除第一种外,均难以控制首次施加的预紧载荷的大小,因此我们选取第一种施加预紧载荷的方式,以达到高精度预紧设置。
通过位移载荷替代切向力,可提高计算结果的精确性。对右侧平板面施加耦合作用,得到耦合点。提取耦合点的位移和反作用力可得出相对应的载荷。左侧平板面施加固定约束,模拟复杂装备的工作状态,使得分析步能够合理运行。
螺栓与平板存在多处接触面:螺栓头部下表面、螺母上表面与平板的接触、螺纹与螺母的接触、平板间的接触。在设定接触面时,需考虑网格质量、接触面的形状、材料的影响。设置三个基础分析步:第一步施加10-100N较小预紧载荷,提高计算结果的收敛性。第二步施加所需预紧载荷。第三步在右侧平板的耦合点施加所需x方向的位移,以模拟切向力的作用。若要进行多组拉伸、压缩循环加载分析,可增加多组分析步。
2、接触边界变化规律研究
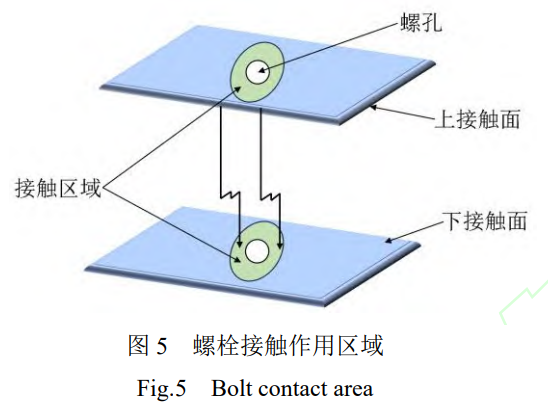
平板间上下结合面接触时,存在局部的接触区域,并非整个面完全接触,如图5所示。主要接触区域为螺孔周围,其压力分布并不完全均匀,受到变形程度、材质的影响。在切向载荷的作用下,接触区域形状逐渐变化。为研究接触区域的边界演化规律,通过有限元方法分析接触边界,构建可表征粘滞、滑移区域的边界函数。
连接表面的滑动状态分为四种:粘滞、微滑、宏滑、销连,无外力作用下,难以引起螺孔周围接触区域移动,称为粘滞状态。微滑、宏滑状态分别指较小、较大载荷下导致接触面相对滑动。销连状态发生弹性形变,影响结构的安全性。施加1000N预紧力,0-829N的切向位移载荷。当切向载荷T≤261N时,无切向力情况螺孔周围呈现圆形粘滞状态,伴随切向力的施加,粘滞区域逐渐减小,接触形态由圆形逐渐演化为椭圆状。当切向载荷T≥261N时,接触区域由粘滞状态逐渐过渡至滑移状态,滑移区域不断从外部向内部延伸,x方向滑移长度缩短,y方向滑移长度增加,接触区域超过平板边界,平板对接触区域产生“截断”现象。
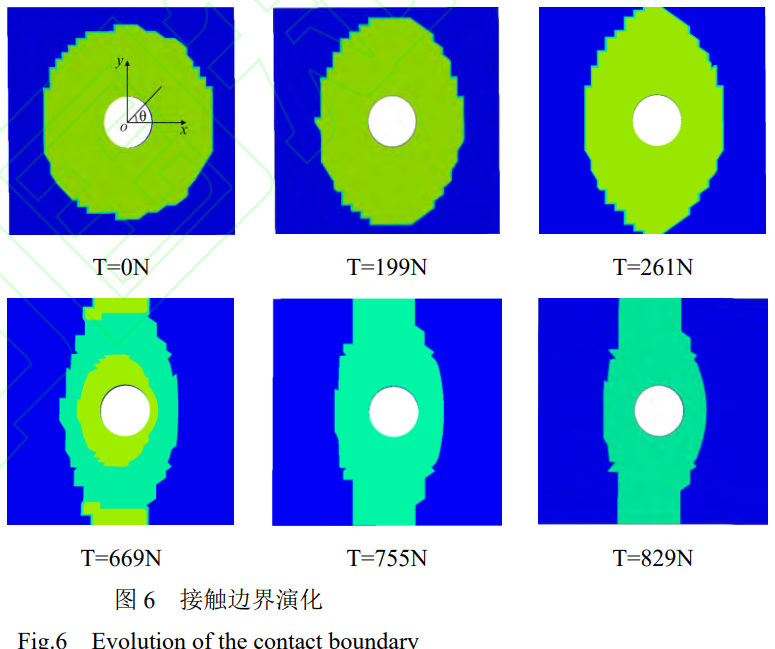
无切向载荷条件下,接触区域呈圆形。切向力作用下,平板间的接触区域可近似为椭圆形。将切向拉力方向定义为x,垂直方向为y,因此,将接触边界形状近似为椭圆状,其公式为
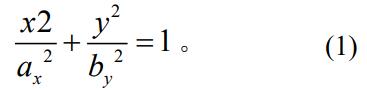
伴随切向位移载荷的增大,接触边界逐渐变化,短半轴缩短,长半轴增加,并超过平板最大宽度。依据有限元模型辨ax、by图7所示。
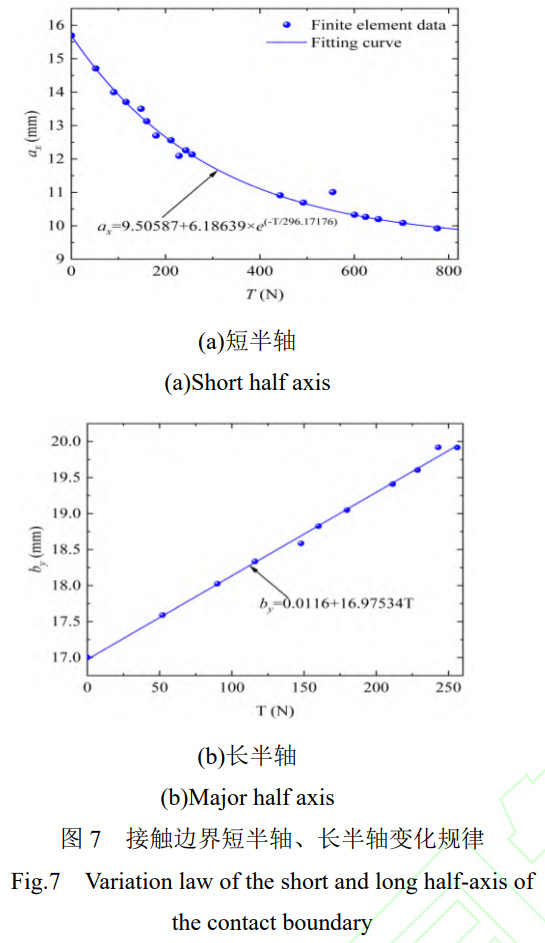
短半轴数值随着切向载荷的增大而减小,长半轴数值随着切向载荷的增大而增大。短半轴函数符合指数变化,长半轴函数符合线性变化,其通用公式为
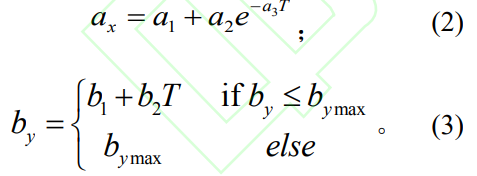
式中:a1、a2、a3、b1、b2均为待辨识参数;bymax为长半轴的最大值,可通过有限元进行参数辨识。
基于式(2)和(3),可通过椭圆面积求得接触面积为
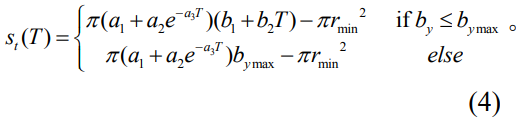
通过长半轴变化公式可知,当T≤261时,接触区域逐渐演化,未达到最大长半轴。当T≥261时,平板结合面出现截断区域,通过上述公式计算的椭圆接触面积偏小。
3、压强变化规律研究
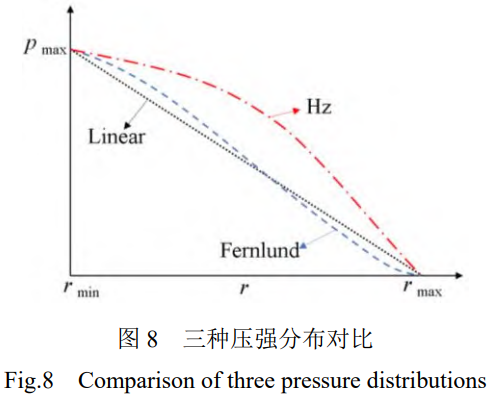
螺栓连接在预紧力作用下,使得平板产生压强,施加切向外载荷导致压强发生变化。基于现有模型函数描述压强分布规律,可表征真实压强分布规律,常用压强分布函数包括:Fernlund压强分布[10]、线性压强分布[5]、赫兹压强分布[11]。通过高精密有限元模型,计算平板间压强分布数值,并通过分布函数简化压强分布规律。
3.1压强分布函数
(1)Fernlund压强分布Motosh将压强与半径表示为4次方程,构建了螺栓连接节点刚度确定方法,其表达式为

式中:
p(r)为压强;r为压强点到螺孔边缘的距离。
基于公式(5),可构建接触表面法向总预紧力的表达式
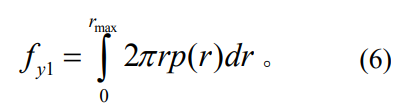
2)线性压强分布
基于压强与半径的因果关系,将分布规律理想化,建立一元线性回归,可采用最小二乘法辨识线性分布中的参数,其表达式为
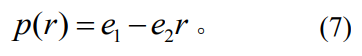
(3)赫兹压强分布
赫兹压强分布基于两个接触物体之间变形假设理论,将模型简化为刚体和面积较小的微凸体接触。压强峰值位移接触中心点,并逐渐向远距离处减小。其压强分布的建立需通过多种物体间假设、简化,与实际情况之间存在误差,其表达式为
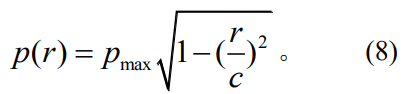
3.2基于有限元的压强函数辨识
有限元模型中施加1000N-15000N法向预紧力,设置切向位移载荷0.05mm,求解上、下平板接触面间压强分布规律。以x方向的螺孔边缘处为原点,即为r=0处,分别提取切向拉力方向压强数值,如图9所示。较小预紧力情况下,三种压强分布函数均表征较好。较大预紧力情况下,三种压强分布函数均在螺孔边缘处存在偏差,螺孔周围为应力集中区域,当预紧载荷较大时,可能会使得材料的力学性能发生改变,例如弹性模量、屈服强度等。由于螺孔的存在,改变了平板的刚度分布,使得螺孔边缘的刚度变化较大。结合面的摩擦系数等因素在较大预紧工况下也会对压强分布产生一定影响,导致压强分布函数在此位置偏差较大。线性压强与Fernlund压强分布在螺孔最远处均存在偏差。而赫兹压强分布偏差较大,不符合有限元中平板接触压强分布规律。
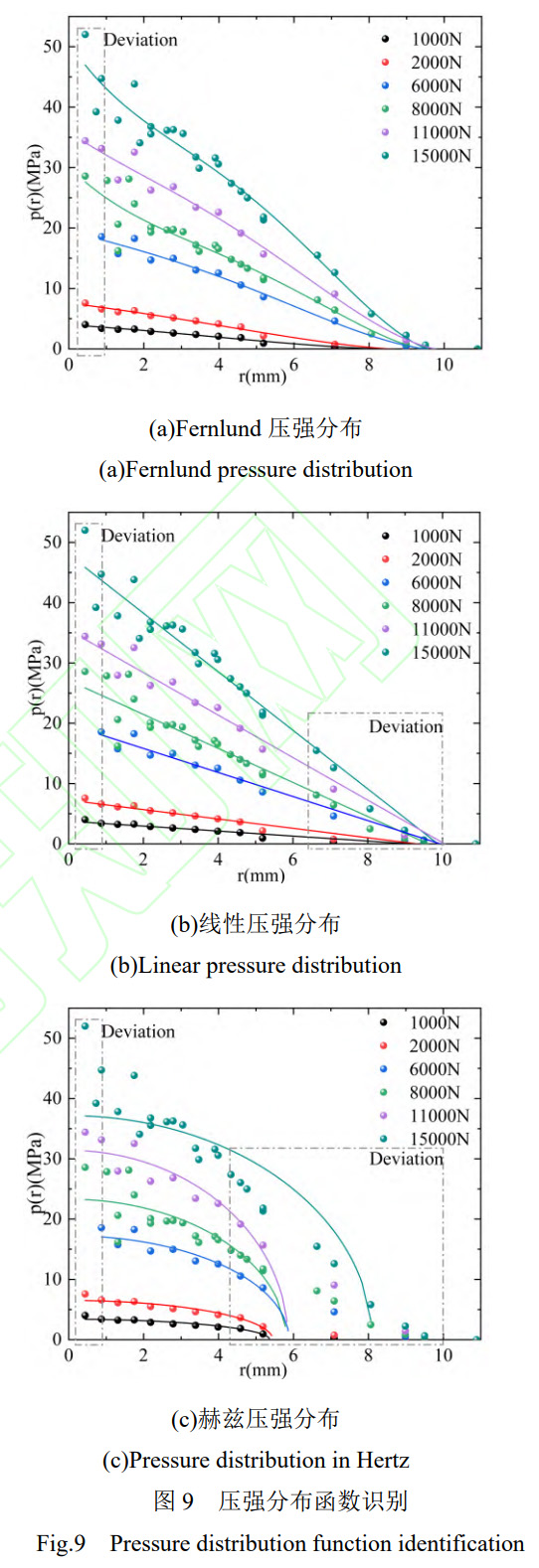
不同初始预紧力下,由偏离区域可知,二者拟合精度相近,均可表征螺栓连接接触表面压强分布。
Fernlund压强分布函数为四次函数,包含5个未知参数,而线性压强分布仅存在2个未知参数,可简化计算。因此,选取参数较少,表征效果较好,结构简单的线性函数作为压强分布函数。
3.3动态压强分布函数研究
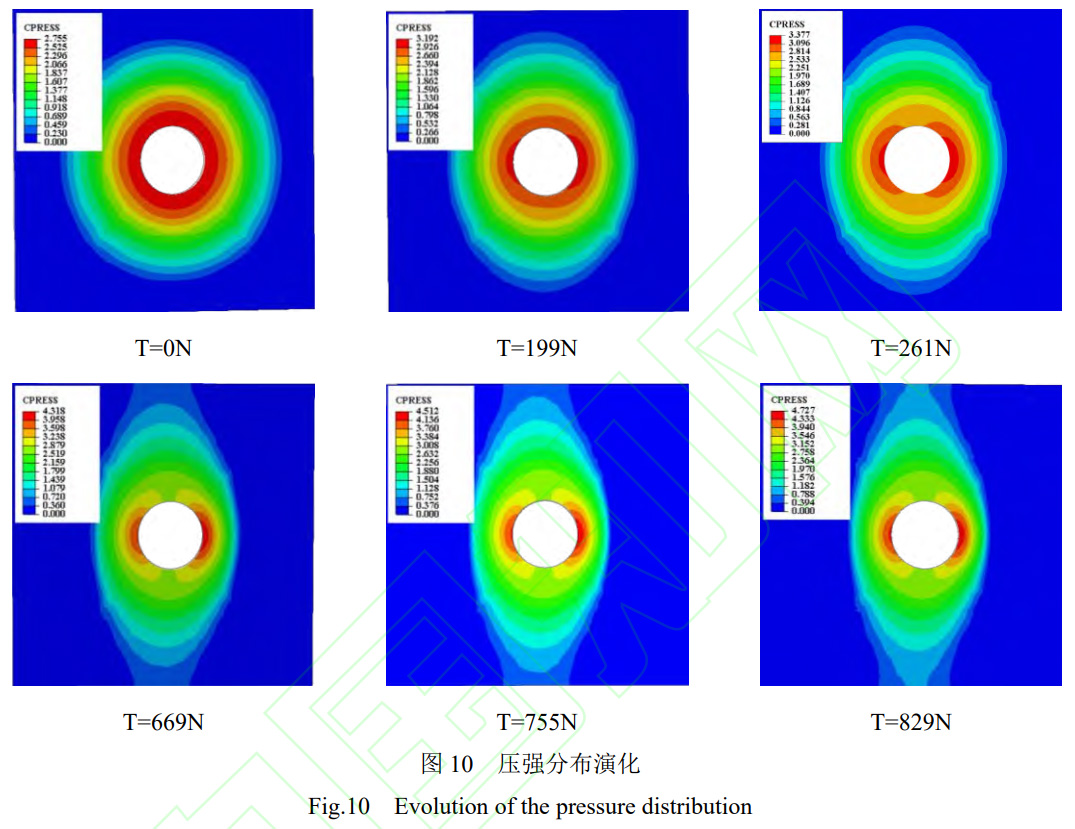
1000N法向预紧载荷、切向0-829N切向外载荷作用下的压强变化如图10所示。较小外载荷作用下,接触区域呈对称分布,较大外载荷作用下,其压强峰值对称分布在y轴两侧。随切向力的增加,压强最大值由2.755MPa变化至4.727MPa,增长率达到71.6%。因此构建平板间动态压强分布规律,需考虑切向外载荷的影响。
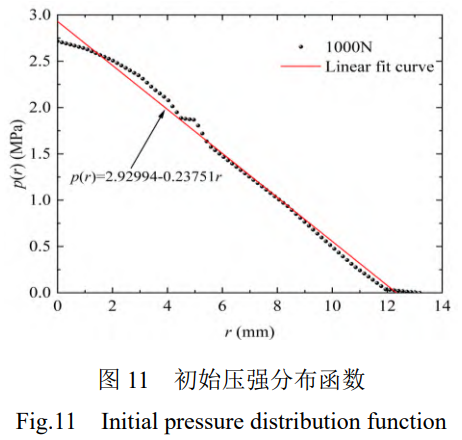
T=0时,1000N法向预紧载荷作用下,基于有限元对线性压强参数1e、2e进行辨识,如图11所示。线性压强分布在r=0mm时的误差为7.9%,在r=4mm时的误差为5.0%,具有较好的拟合效果。
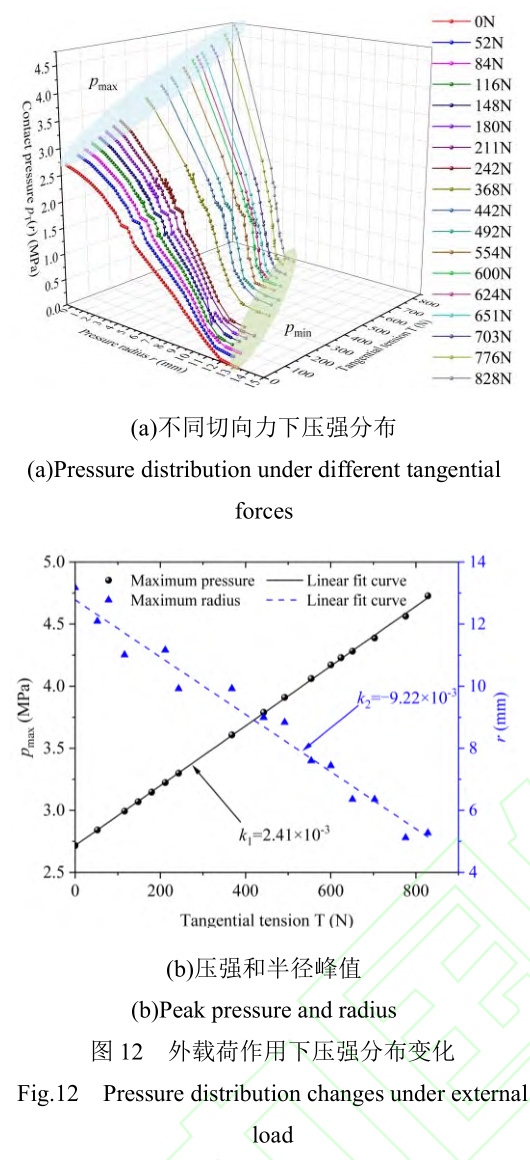
线性压强分布函数可描述平板间压强演化规律,而切向力的改变会导致最大压强值、压强最大半径变化,对x轴正方向的压强展开有限元分析,如图12(a)所示。当压强半径r=0时,压强达到峰值,随压强半径
的增加,压强值逐渐线性减小至0。其中压强峰值区域随切向拉力线性增加,达到压强零值的半径随切向拉力线性降低,如图12(b)所示。因此,需对线性压强分布函数开展横向、纵向压强调整,以弥补切向外载荷造成的压强变化。
为建立不同切向拉力情况下的动态变化分布函数,需添加线性压强函数纵向演化系数。压强峰值与切向拉力存在线性关系,因此可将压强分布函数p(r)等比倍增,其公式为
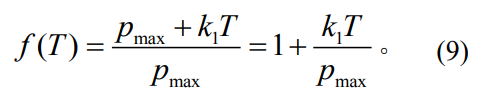
式中:pmax为T=0时的压强峰值。
随切向外力的增加,压强值达到零值时的半径线性减小,通过有限元提取最大半径的距离,可得出斜率值。因此,依据线性函数对压强分布函数进行横向调整,其横向半径长度之比为式中:
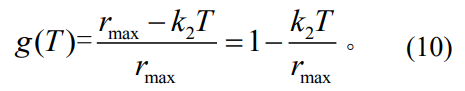
rmax为T=0时的最大接触半径。
因此,随切向载荷变化的线性压强分布函数为
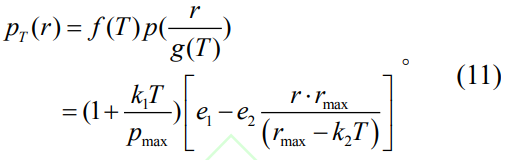
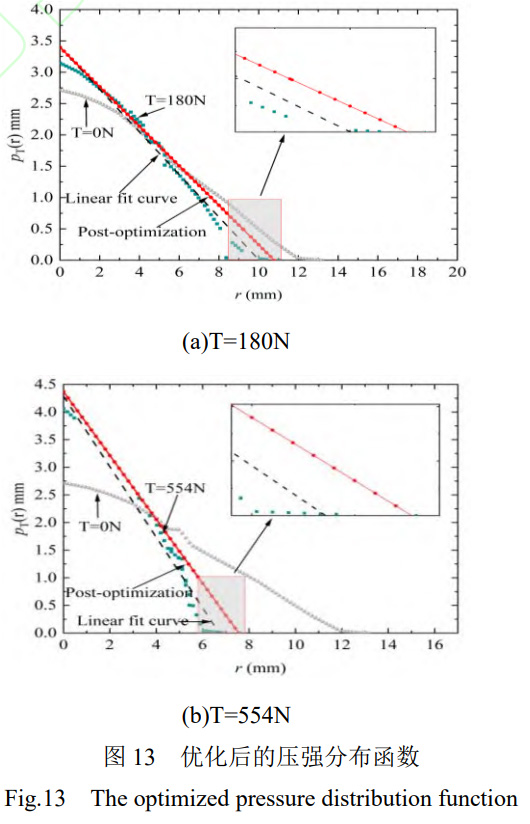
T=180N、554N切向拉力下的压强分布曲线,如图13所示。当压强为峰值时,优化后的动态压强分布函数与原动态压强的拟合函数具有较高的重叠度。当压强为零时,优化后的函数半径较大于原函数的拟合曲线,其半径分别为:10.77675mm、10.02866mm和7.5789mm、6.7168mm,两条曲线在压强为零时存在一定偏差,但总体拟合效果较好,证明了本文动态线性压强分布函数的准确性。
4、结束语
本文建立了简化的螺栓和等效平板有限元模型,研究了螺栓连接结构结合面的接触边界和压强分布演化规律。结果表明:
(1)结合面接触区域受切向力的影响发生动态变化。当切向载荷较小时,初始状态接触的螺孔周围呈现圆形粘滞状态,伴随切向力的施加,粘滞区域逐渐减小,接触形态由圆形逐渐演化为椭圆状,未达到最大长半轴。当切向载荷较大时,接触区域由粘滞状态逐渐过渡至滑移状态,滑移区域不断从外部向内部延伸,x方向滑移长度缩短,y方向滑移长度增加,接触区域超过平板边界,平板对接触区域产生“截断”现象。
(2)切向载荷作用下,结合面各点的压强发生变化。采用线性压强分布函数,对曲线进行横、纵调整,得到表征效果较好、参数较少的线性动态压强分布函数。为螺栓连接结构的性能评估提供理论支撑。
参考文献(References)
[1] WANG Shengao, ZHU Min, CAO Hongjun, et al. Contact Pressure Distribution and Pressure Correction Methods of Bolted Joints under Mixed-Mode Loading[J]. Coatings, 2022, 12(10): 1516.
[2] 宋道远, 徐兴华, 邱少华, 等.基于改进 YOLOv5 的螺 栓 紧 固 件 检 测 [J]. 海 军 工 程 大 学学 报 , 2024,36(3):72-76.
SONG Daoyuan, XU Xinghua, QIU Shaohua, et al. Bolt Fasteners Detection Based on Improved YOLOv5 [J]. Journal of Naval University of Engineering, 2024,36(3):72-76. (in Chinese)
[3] LU Xiaohan, ZHU Min, LI Chao, et al. Prediction of Pre-Loading Relaxation of Bolt Structure of Complex Equipment under Tangential Cyclic Load [J]. Sensors, 2024, 24(11): 3306.
[4] ZHANG Weihong, LI Jiajia, GAO Tong. Topology Optimization of Elastic Contact Problems with Maximum Contact Pressure Constraint [J]. Structural and Multidisciplinary Optimization, 2022,65(4): 106.
[5] ZHAO Binbin, WU Fayong, SUN Kepeng, et al. Study on Tangential Stiffness Nonlinear Softening of Bolted Joint in Friction-Sliding Process [J]. Tribology International, 2021, 156:106856.
[6] WANG Shengao, ZHU Min, XIE Xin, et al. Finite Element Analysis of Elastoplastic Elements in the Iwan Model of Bolted Joints [J]. Materials, 2022, 15: 5817.
[7] LI Dongwu, BOTTO Daniele, XU Chao, et al. A Micro-Slip Friction Modeling Approach and Its Application in Underplatform Damper Kinematics [J]. International Journal of Mechanical Sciences, 2019, 161-162: 105029.
[8] LI Dongwu, XU Chao, BOTTO Daniele, et al. A Fretting Test Apparatus for Measuring Friction Hysteresis of Bolted Joints [J]. Tribology International, 2020, 151: 106431.
[9] 赵永武, 吕彦明, 蒋建忠. 新的粗糙表面弹塑性接触 模型[J]. 机械工程学报, 2007,43(3): 95-101.
ZHAO Yongwu, LYU Yanming, JIANG Jianzhong. New Elastic-plastic Contact Model of Rough Surface[J]. Journal of Mechanical Engineering, 2007,43(3): 95-101. (in Chinese)
[10] MOTOSH N. Determination of Joint Stiffness in Bolte Connections [J]. Journal of Engineering for Industry, 1976, 98(3): 858-861.
[11] JOHNSON K L. Contact Mechanics [M]. Cambridge: Cambridge University Press, 1985:84-106.
相关链接